440. 字典序的第K小数字 #
链接 #
题目 #
给定整数 n 和 k,返回 [1, n] 中字典序第 k 小的数字。
示例 1:
输入: n = 13, k = 2 输出: 10 解释: 字典序的排列是 [1, 10, 11, 12, 13, 2, 3, 4, 5, 6, 7, 8, 9],所以第二小的数字是 10。
示例 2:
输入: n = 1, k = 1 输出: 1
提示:
1 <= k <= n <= 109
解答 #
如图,我们可以把它转化寻找深度优先遍历前缀树的第 k 个节点。在每个节点我们都要做一个决策:是继续往子节点走,还是往兄弟节点走。
在我图的例子中,考虑 N=123,k=2 或 k=15 的情况。
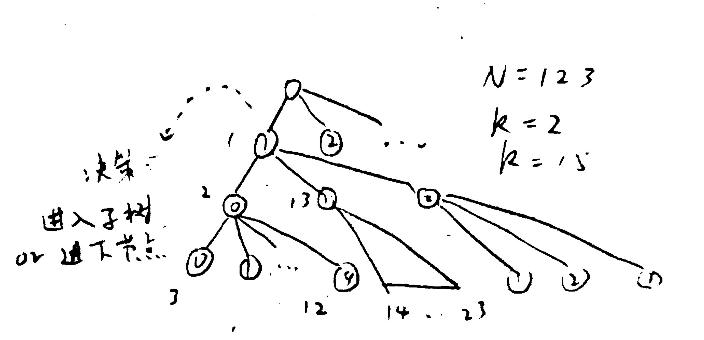
这个决策取决于子树能容纳多少个节点,k 是否在其范围内。
看上图,在 k=1 对应的节点处,我们尝试计算子树的大小(不含自己)
- 自己的直接子节点有 0、1、2,算 3 个,
- 这些子节点的子节点,对 0、1 而言各 10 个,对 2 而言有 3 个,一共 23 个
上面加起来一共 3+23=27 个,所以 k=2 在这个子树内。往下走。我们来到了 k = 2 的结点,结束,得到值:10.
如果目标 k = 15,我们在 k=2 的节点继续决策:
- 子节点 10 个
那么最后一个子节点应该是 k = 2+10 = 12 的节点,因此在 k=2 时应该走到下一个兄弟节点。来到 k=13 的节点。
k=13 的节点,其子节点 10 个,15 < 13+10,因此可以知道 k=15 在这个子树内。往下走,第二个节点就是了,其字符串值:111. 得到答案。
class Solution:
def findKthNumber(self, n: int, k: int) -> int:
def countSteps(prefix, n):
"""计算从prefix到下一个前缀之间的步数,即前缀下的数字总数"""
steps = 0
first = prefix
last = prefix
while first <= n:
steps += min(n + 1, last + 1) - first
first *= 10
last = last * 10 + 9
return steps
current = 1
k -= 1 # 减去根节点
while k > 0:
steps = countSteps(current, n)
if steps <= k:
# 不在当前前缀下,向右移动
k -= steps
current += 1
else:
# 在当前前缀下,向下深入
k -= 1 # 跳过当前节点
current *= 10
return current